Die Figur enthält 64 Dreiecke. Ein Lösungsweg besteht im Durchzählen aller Dreiecke. Cleverer ist jedoch die Lösung, bei der Kombinatorik zum Einsatz kommt.
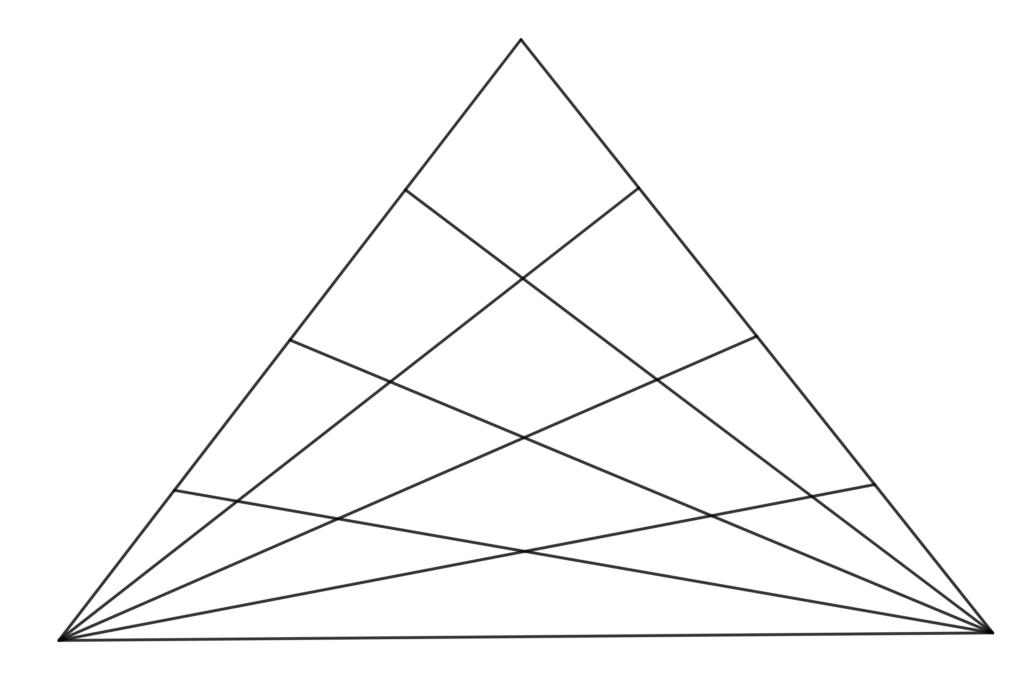
Beim Durchzählen der Dreiecke ist die Gefahr groß, eines zu übersehen oder doppelt zu zählen. Weniger fehlerträchtig ist eine allgemeine Lösung.
Die Figur besteht aus insgesamt neun Geraden, wobei nur die Teile der Geraden sichtbar sind, die zwischen Schnittstellen mit anderen Geraden liegen. Wir können die Frage nun allgemein formulieren: Wie viele Dreiecke bilden neun Geraden, sofern sich darunter keine befinden, die parallel zueinander sind? Und sofern durch alle Schnittpunkte dieser Geraden immer nur zwei Geraden verlaufen, was bei der Figur oben nicht zutrifft?
In diesem allgemeinen Fall wird die Aufgabe zu einem kombinatorischen Problem: Drei beliebig ausgewählte Geraden bilden immer ein Dreieck, solange es keine parallelen Geraden gibt. Die Frage lautet dann: Wie viele verschiedene Kombinationen von drei Geraden existieren, die man aus den neun Geraden auswählen kann?
Die Antwort ist einfach: Es ist der sogenannte Binomialkoeffizent 9 über 3 – also 9!/(3! * (9-3)!) = 9*8*7/3*2 = 84.
Doch das ist noch nicht die gesuchte Lösung, weil es ja zwei Schnittpunkte gibt, durch die mehr als zwei Geraden verlaufen. Dadurch sinkt die Zahl der durch die Geraden gebildeten Dreiecke.
Immer wenn drei Geraden einen gemeinsamen Schnittpunkt haben, können diese drei Geraden kein Dreieck mehr bilden. Also müssen wir alle Kombinationen von drei verschiedenen Geraden ermitteln, die einen gemeinsamen Schnittpunkt haben und diese Anzahl von den oben berechneten 84 Kombinationen abziehen.
Weil an jedem der zwei Punkte fünf Geraden einander schneiden, existieren pro Punkt 5 über 3 = 5*4*3/3*2 = 10 Kombinationen von drei Geraden. Subtrahieren wir diese insgesamt 20 Kombinationen von 84, kommen auf die Lösung von 64 Dreiecken.
