Wir konstruieren aus dem Dreieck ABC ein Parallelogramm ABCB’. Dazu drehen wir das Dreieck ABC um den Punkt M um 180 Grad.
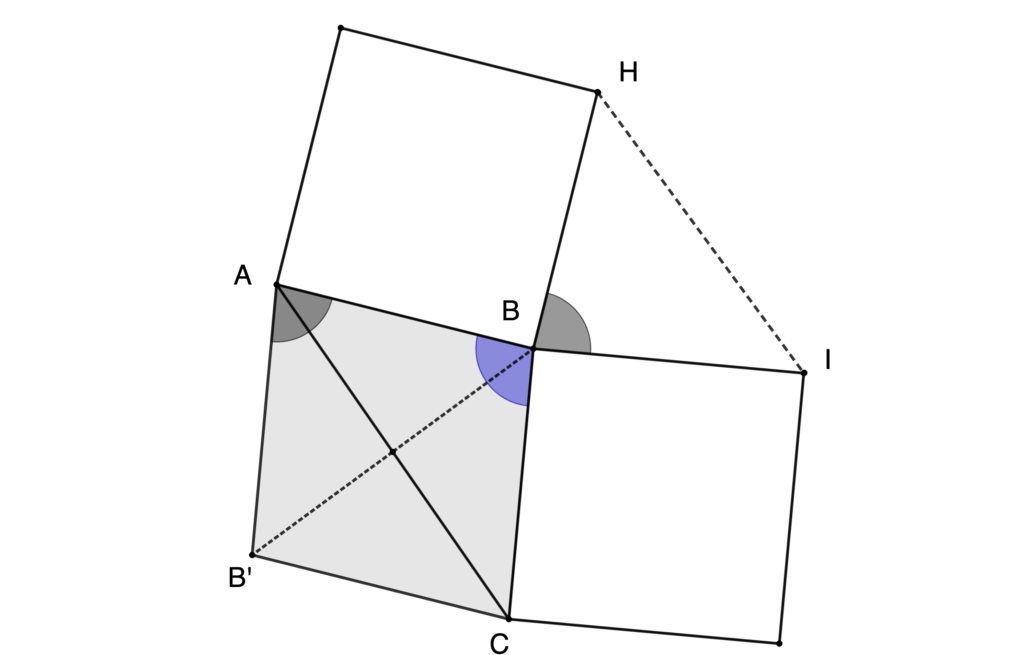
Es ist nun nicht mehr allzu schwer zu zeigen, dass das Dreieck ABB’ kongruent zum Dreieck HIB ist. Der blau gekennzeichnete Innenwinkel des Dreiecks ABC am Punkt B soll die Größe alpha haben. Dann hat der grau gekennzeichnete Winkel am Punkt B die Größe 180 – alpha.
Aber auch der Innenwinkel des Parallelogramms ABCB’ am Punkt A hat die Größe 180 – alpha. Denn die Summe zweier benachbarter Innenwinkel eines Parallelogramms beträgt stets 180 Grad – und alpha ist ein benachbarter Innenwinkel zum Winkel am Punkt A.
Zudem gilt: AB = BH sowie AB’ = BI. Deshalb stimmen die beiden Dreiecke ABB’ und HIB in zwei Seiten und dem eingeschlossenen Winkel überein. Beide Dreiecke müssen deshalb kongruent sein.
Damit steht auch fest, dass die doppelte Seitenhalbierende BB’ genauso lang ist wie die Strecke HI. Oder anders gesagt: HI ist doppelt so lang wie die Seitenhalbierende.
